spherical coordinate 질문 (coordinate, sine, cosine, unit vector, change, plane, projection, vector, dynamics, concept)

질문 요약

보라색 글씨인 sin(화이)이 사실 cos(화이) 아닌가요? 풀이과정에 오류가 있는 것 같습니다. #spherical_coordinate #cos https://file.unistudy.co.kr/Data/SEDATA/gooden__20240508213349.png

답변 요약

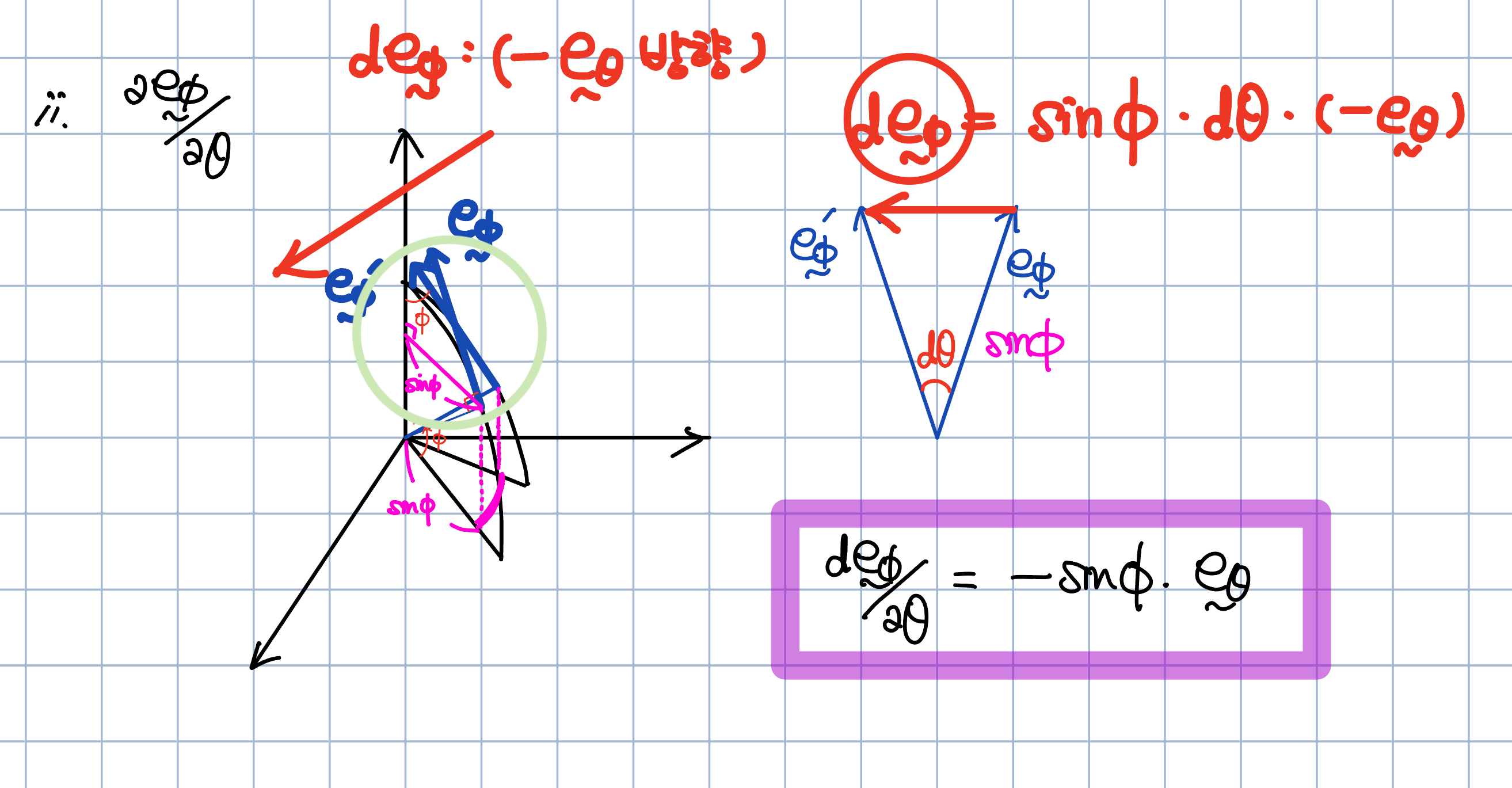
Φ 단위벡터의 θ에 따른 변화량을 유도하는 부분입니다. Φ 단위벡터의 xy평면에 정사영을 표현하면 sinΦ가 맞습니다. r벡터에 대한 정사영과 혼동하지 않도록 주의하세요. 동역학에서 중요한 개념이니 잘 이해해두세요. https://godjunpyo.com/wp-content/uploads/kboard_attached/8/202405/6646f0d6d071f2347010.png

원본 바로가기 >>>

 

Unsplash 추천 이미지 (키워드 : coordinate, sine, cosine, unit vector, change, plane, projection, vector, dynamics, concept )

 

spherical coordinate 질문

여러분, 안녕하세요! 오늘은 구면좌표계(spherical coordinate)에 대한 질문과 답변을 다루어보려고 합니다. 구면좌표계는 물리학과 공학에서 자주 사용되는 좌표계로, 구의 표면을 따라 위치를 지정하는 데 유용합니다. 특히, 동역학 문제를 다룰 때는 구면좌표계가 매우 중요합니다. 이번 포스트에서는 질문과 함께 이에 대한 답변을 자세히 설명하겠습니다.

질문: 보라색 글씨인 sin(Φ)이 사실 cos(Φ) 아닌가요? 풀이과정에 오류가 있는 것 같습니다. #spherical_coordinate #cos

답변

Φ 단위벡터의 θ에 따른 변화량을 유도하는 부분입니다. Φ 단위벡터의 xy평면에 정사영을 표현하면 sinΦ가 맞습니다. r벡터에 대한 정사영과 혼동하지 않도록 주의하세요. 동역학에서 중요한 개념이니 잘 이해해두세요.

추가 설명

구면좌표계에서 위치를 나타내기 위해 사용하는 세 가지 좌표는 \( r \), \( \theta \), \( \phi \)입니다. 여기서 각 좌표의 의미는 다음과 같습니다:

1. \( r \): 원점에서 점까지의 거리
2. \( \theta \): 양의 z축에서 점까지의 벡터가 만드는 각도 (polar angle)
3. \( \phi \): xy평면에서 x축과 점의 투영이 만드는 각도 (azimuthal angle)

이제 Φ 단위벡터의 xy평면에 대한 정사영을 이해하기 위해 수학적으로 접근해보겠습니다. 구면좌표계에서 임의의 점 P의 좌표는 다음과 같이 표현됩니다:

Cartesian 좌표계로 변환하면:

\( x = r \sin \theta \cos \phi \)
\( y = r \sin \theta \sin \phi \)
\( z = r \cos \theta \)

여기서 중요한 점은 θ와 φ가 변할 때 각 단위벡터가 어떻게 변하는지 이해하는 것입니다. 특히, Φ 단위벡터는 다음과 같이 정의됩니다:

\( \hat{\phi} = -\sin \phi \hat{i} + \cos \phi \hat{j} \)

이때, xy평면에 정사영을 구하면 \( \sin \phi \)가 포함된 항이 나타납니다. 이는 Φ 단위벡터의 xy평면에 대한 정사영이므로, sinΦ가 맞습니다. 만약 r벡터에 대한 정사영을 구하려고 한다면 다른 결과가 나올 수 있습니다. 그러므로 문제 풀이 과정에서 실수하지 않도록 주의해야 합니다.

유도 과정

Φ 단위벡터의 θ에 따른 변화량을 유도하는 과정은 다음과 같습니다:

1. Φ 단위벡터를 Cartesian 좌표계로 변환합니다.
2. 이를 θ에 대해 미분합니다.
3. 미분 결과를 다시 구면좌표계로 변환합니다.

구체적인 유도 과정은 다음과 같습니다:

\[ \hat{\phi} = -\sin \phi \hat{i} + \cos \phi \hat{j} \] \[ \frac{\partial \hat{\phi}}{\partial \theta} = -\sin \phi \frac{\partial \hat{i}}{\partial \theta} + \cos \phi \frac{\partial \hat{j}}{\partial \theta} \] \[ \frac{\partial \hat{i}}{\partial \theta} = \cos \theta \cos \phi \hat{i} + \cos \theta \sin \phi \hat{j} - \sin \theta \hat{k} \] \[ \frac{\partial \hat{j}}{\partial \theta} = -\sin \phi \hat{i} + \cos \phi \hat{j} \]

이를 종합하면 Φ 단위벡터의 θ에 따른 변화량을 구할 수 있습니다. 이 과정은 다소 복잡하지만, 물리적으로 매우 중요한 의미를 가지므로 정확히 이해하는 것이 중요합니다.

결론

구면좌표계는 동역학 문제를 해결하는 데 있어 매우 중요한 도구입니다. 특히, Φ 단위벡터의 xy평면에 대한 정사영을 정확히 이해하는 것이 중요합니다. 이번 포스트에서 다룬 내용을 통해 여러분이 구면좌표계에 대한 이해를 더욱 높일 수 있기를 바랍니다. 추가적인 질문이 있다면 언제든지 댓글로 남겨주세요!

키워드: spherical coordinate, sin, cos, Φ 단위벡터, θ에 따른 변화량, xy평면, 정사영, r벡터, 동역학, 개념

유니스터디 바로가기 : https://www.unistudy.co.kr/megauni.asp

학습Q&A 바로가기 : https://www.unistudy.co.kr/community/qna_list.asp