질문 요약
동역학 15강 3.13번 문제에서 장력이 한 일에 대한 이해가 어려워서 일의 정의를 활용하여 장력이 한 일을 유도하려고 하는데 도움이 필요합니다.
답변 요약
안녕하세요. 에너지 보존 법칙을 사용하여 블록의 속도를 계산하는 문제에 대한 추가 설명을 해드리겠습니다. 스프링에 연결된 블록은 위치 A에서 위치 B까지 이동하며 외부 힘과 텐션 힘에 의해 운동합니다. 블록의 속도를 구하기 위해 위치 A와 B에서의 잠재 에너지 차이를 이용하여 운동에너지를 계산하고, 속도를 구합니다. 계산 결과로 블록의 위치 B에서의 속도는 약 2m/s입니다. 자세한 풀이과정은 이미지로 전해드립니다 : https://godjunpyo.com/wp-content/uploads/kboard_attached/8/202403/65ef2edf0cde73202101.png
Unsplash 추천 이미지 (키워드 : Dynamics, Tension, Work, Law of Energy Conservation, Block, Velocity, Position A, Position B, Potential Energy, Kinetic Energy. )
동역학에서 장력이 한 일에 대한 궁금증 해결
안녕하세요. 동역학을 공부하면서 장력이 한 일에 대한 개념에 대해 궁금증을 가진 분들이 많습니다. 특히, 동역학 15강에서 다룬 예제 3.13번 문제와 관련하여 장력이 한 일을 어떻게 계산하는지에 대한 질문을 자주 접하게 됩니다. 이러한 궁금증을 해소하기 위해 일의 정의를 바탕으로 장력이 한 일을 어떻게 계산하는지 상세하게 설명하도록 하겠습니다.
일의 정의와 장력이 한 일
먼저, 일의 정의부터 짚고 넘어가야 합니다. 물리학에서 일(Work)은 힘이 물체를 움직이게 했을 때 수행된 에너지의 양으로 정의됩니다. 수학적으로 일은 힘(F)과 힘이 가해진 방향으로의 이동 거리(d)의 곱으로 표현됩니다. 즉, 일 \(W\)은 다음과 같이 계산할 수 있습니다.
\[ W = F \times d \]
여기서 중요한 점은 힘과 이동 거리가 벡터량이라는 것입니다. 따라서, 실제로는 힘의 방향과 이동 방향이 일치할 때 가장 많은 일이 수행됩니다. 이를 고려하여 장력이 한 일을 계산하면, 장력 \(T\)와 장력의 방향으로의 이동 거리 \(\Delta x\)를 이용하여 계산할 수 있습니다.
따라서, 장력이 한 일 \(W_t\)는 다음과 같이 표현됩니다.
\[ W_t = T \times \Delta x \]
예제 3.13번 문제의 장력이 한 일 계산
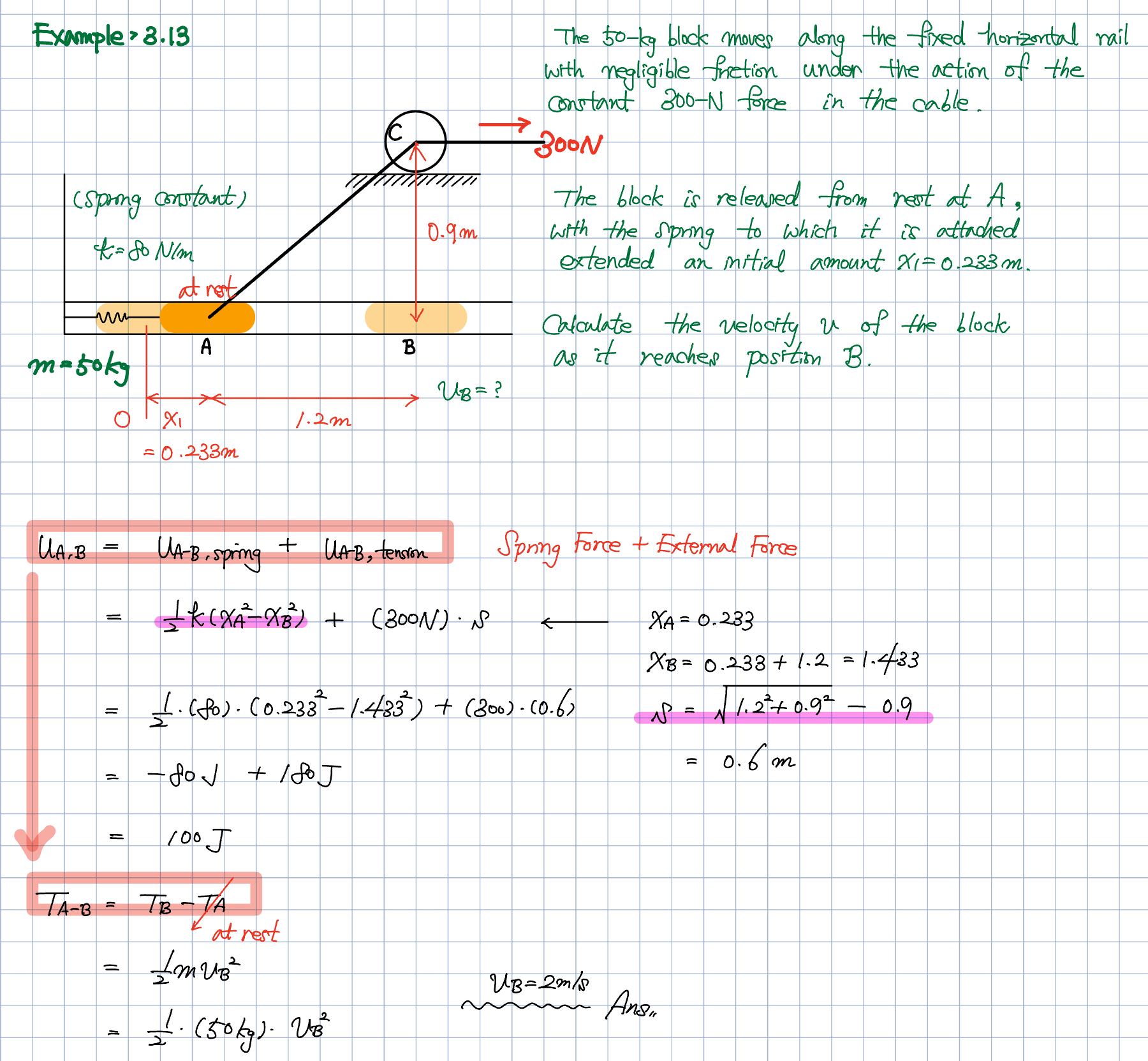
이제 동역학 15강에서 다룬 예제 3.13번 문제를 살펴보겠습니다. 문제에서는 블록이 스프링에 연결되어 위치 A에서 위치 B까지 이동한다고 했을 때, 장력이 한 일을 계산하라고 합니다. 장력이 300N이고, 블록의 이동 거리가 1.5m에서 0.9m라면, 장력이 한 일은 다음과 같이 계산할 수 있습니다.
\[ W_t = 300N \times (1.5m - 0.9m) = 300N \times 0.6m = 180J \]
즉, 장력이 블록을 0.6m만큼 이동시키는 데에 180J의 일을 수행했다는 의미입니다.
추가 설명과 자료
에너지 보존 법칙을 사용하여 블록의 속도를 계산하는 과정에서 장력이 한 일을 이해하는 것은 매우 중요합니다. 블록의 위치 A와 위치 B에서의 잠재 에너지 차이를 이용하여 운동에너지를 계산하고, 이를 통해 속도를 구할 수 있습니다. 계산 결과로 블록의 위치 B에서의 속도는 약 2m/s로 나타납니다.
자세한 풀이과정은 아래 이미지를 참조해 주세요.
또한, 질문 내용에 대한 보충 자료는 다음 링크에서 확인할 수 있습니다.
질문 보충 이미지동역학 공부에 있어서 장력이 한 일에 대한 이해는 중요한 개념 중 하나입니다. 이 글을 통해 장력이 한 일에 대한 궁금증이 해소되기를 바랍니다. 추가적인 궁금증이 있다면 언제든지 질문해 주시기 바랍니다.
유니스터디 바로가기 : https://www.unistudy.co.kr/megauni.asp
학습Q&A 바로가기 : https://www.unistudy.co.kr/community/qna_list.asp







0 댓글