일과 내적의 관계에 대한 이해 (physics, vector mathematics, force and displacement, integral calculus, work calculation, physics graph)

질문 요약

32:39초에서 sigma W= integral (f내적r)이라고 설명되어 있는데 이해가 안 됩니다. 넓이를 구할 때 보통 밑변 곱하기 높이로 하는데 왜 내적으로 표시되는지 궁금합니다. 그래프에서는 힘을 위치 변화 방향과 수평한 상태로 가정하고 있어서 cos0은 1이니까, integral에서 내적을 그냥 곱하기처럼 봐도 되는지 궁금합니다.

답변 요약

일을 계산할 때는 힘의 성분 중 변위 방향과 나란한 성분만 고려합니다. 그래서 그래프에서 보여주는 힘은 모든 힘을 의미하는 것이 아니라, 변위 방향에 평행한 성분만 보여줍니다. 힘-위치 그래프는 방향성을 포함하므로, 위치 변화 방향에 따라 일의 부호가 달라질 수 있습니다. 따라서, 힘과 변위의 내적을 적분하여 구하는 것은 일의 정의에 부합하며, 그래프에서의 힘은 위치 변화 방향과 나란한 성분만을 나타낸다고 이해하시면 됩니다.

원본 바로가기 >>>

 

Unsplash 추천 이미지 (키워드 : physics, vector mathematics, force and displacement, integral calculus, work calculation, physics graph )

 

일과 내적의 관계에 대한 이해

물리학에서 일을 계산할 때, 우리는 주로 힘과 변위의 관계를 고려합니다. 이는 벡터의 내적을 통해 설명될 수 있습니다. 일반적으로 일을 계산할 때, 힘 벡터와 변위 벡터 간의 내적을 취함으로써 일을 정의합니다. 이번 블로그에서는 왜 내적을 사용하여 일을 계산하는지에 대해 자세히 알아보겠습니다.

힘과 변위의 내적

힘 \( \mathbf{F} \)과 변위 \( \mathbf{r} \)는 모두 벡터입니다. 벡터의 내적은 두 벡터 사이의 각도와 크기를 반영하여 계산됩니다. 내적의 정의에 따르면:

\[ \mathbf{F} \cdot \mathbf{r} = |\mathbf{F}| |\mathbf{r}| \cos \theta \]

여기서 \( \theta \)는 힘 벡터와 변위 벡터 사이의 각도입니다. 즉, 힘이 변위와 같은 방향으로 작용할 때, 즉 \( \theta = 0 \)일 때, \( \cos \theta = 1 \)이므로 내적은 단순히 두 벡터의 크기의 곱이 됩니다.

일의 정의와 계산

일은 물리적으로 힘이 물체를 이동시키는 과정에서 에너지를 전달하는 양입니다. 일의 정의는 다음과 같이 적분으로 나타낼 수 있습니다:

\[ W = \int \mathbf{F} \cdot d\mathbf{r} \]

여기서 \( d\mathbf{r} \)는 미소 변위를 나타내며, \(\mathbf{F} \cdot d\mathbf{r}\)는 미소 변위에 따른 미소 일입니다. 따라서 전체 일 \( W \)는 변위 경로에 따라 힘과 변위의 내적을 적분하여 계산됩니다.

왜 내적을 사용하는가?

힘은 벡터이므로, 모든 방향으로 작용할 수 있습니다. 따라서 우리는 변위 방향과 나란한 힘의 성분만을 고려해야 합니다. 내적을 사용하면 변위 방향과 나란한 힘의 성분, 즉 실제로 물체를 이동시키는 힘의 성분만을 계산할 수 있습니다. 이는 물리학적으로 일의 정의에 부합합니다.

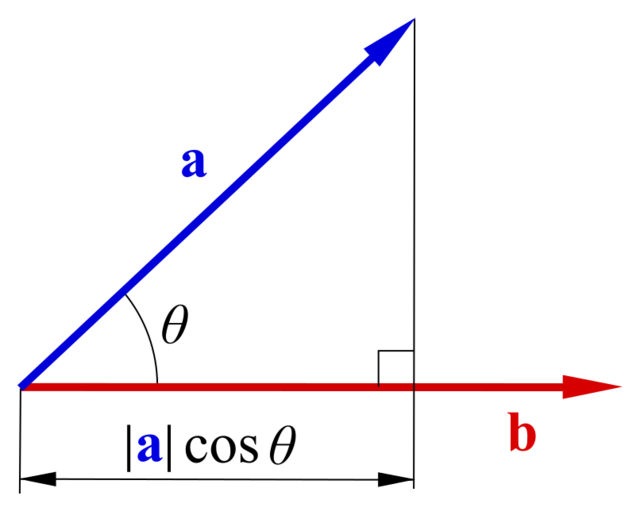
위 이미지에서 볼 수 있듯이, 벡터의 내적은 두 벡터의 크기와 두 벡터 사이의 각도의 코사인 값의 곱으로 표현됩니다. 따라서, 변위 방향과 평행한 힘의 성분만 고려하는 것이 가능합니다.

변위 방향과 일의 부호

힘과 변위의 내적은 방향성을 고려하기 때문에, 변위의 방향에 따라 일의 부호가 달라질 수 있습니다. 예를 들어, 힘이 변위와 같은 방향이면 양의 일이 되고, 반대 방향이면 음의 일이 됩니다. 이는 외부로부터 시스템으로 에너지가 전달되는지 또는 시스템으로부터 외부로 에너지가 전달되는지를 나타냅니다.

결론

결론적으로, 일을 계산할 때 변위 방향과 나란한 힘의 성분만을 고려하기 위해 벡터의 내적을 사용합니다. 내적을 통해 힘의 크기, 변위의 크기, 그리고 두 벡터 사이의 각도까지 고려하여 물리적인 일을 보다 정확하게 계산할 수 있습니다. 이는 물리학에서의 일의 개념을 보다 명확하게 이해하는 데 중요한 역할을 합니다.

유니스터디 바로가기 : https://www.unistudy.co.kr/megauni.asp

학습Q&A 바로가기 : https://www.unistudy.co.kr/community/qna_list.asp