Control Volume로 잡은 미소체적 내 압력 계산 방법에 대해 궁금합니다 (Fluid dynamics, Control Volume, Microscale, Pressure, Calculation, Bernoulli's equation, Fluid flow, Absolute pressure, Flow direction, Area change)

질문 요약

유체역학 강의를 듣는 중에 Control Volume로 잡은 미소체적 내 압력을 계산할 때, 식이 1/2 * dp * dA로 주어졌는데 이 부분이 이해가 되지 않습니다. dp의 삼각형 형태를 dA만큼 늘어난 것으로 이해해야 하는데, 이에 대한 설명을 요청드립니다.

답변 요약

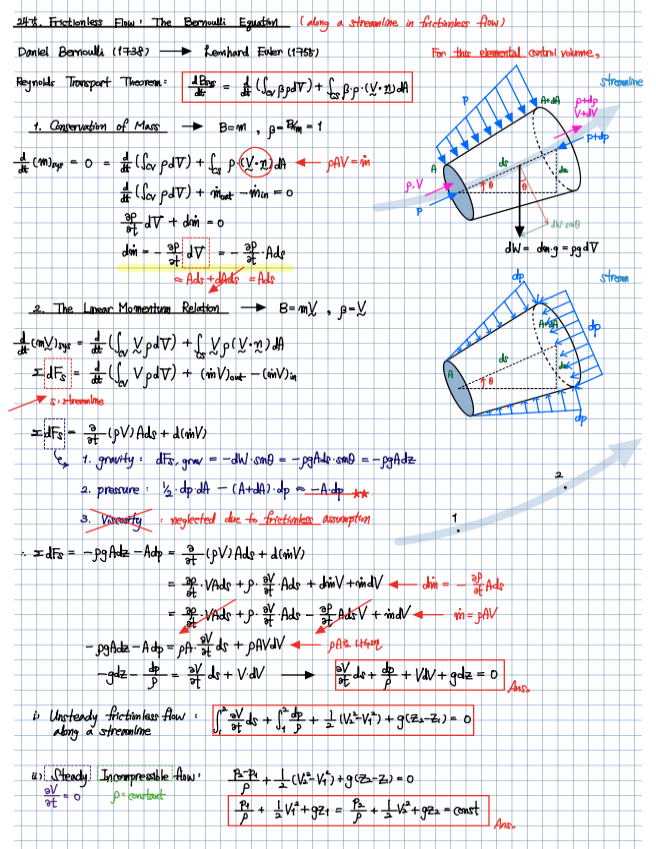
안녕하세요. 베르누이 방정식을 이해하는데 어려운 부분이 dp가 -Adp로 근사되는 이유입니다. 유체의 흐름을 따라서 작은 Control Volume을 상상해보면, CV의 양 끝에서 작용하는 압력의 차이에 의한 힘은 Adp입니다. 순압력 F_s,press는 흐름 방향의 압력 차이를 나타내는데, 이는 순압력을 구하기 위해 앞뒤 면적의 압력을 dp로 곱한 후, dp에 의한 압력 차이로 -Adp로 근사됩니다. 이는 흐름 방향의 순압력을 나타내며, 면적 변화(dA)는 무시할 만큼 작기 때문입니다. 이해를 돕기 위해 다소 복잡하지만 그림으로 전해드립니다. (이미지 : https://godjunpyo.com/wp-content/uploads/kboard_attached/7/202403/65ef52efb219a3863909.png)

원본 바로가기 >>>

 

Unsplash 추천 이미지 (키워드 : Fluid dynamics, Control Volume, Microscale, Pressure, Calculation, Bernoulli's equation, Fluid flow, Absolute pressure, Flow direction, Area change )

 

Control Volume을 이용한 미소체적 내 압력 계산 방법

유체역학을 공부하며 유체의 흐름과 관련된 다양한 현상을 이해하는 것은 매우 중요합니다. 이 과정에서 Control Volume(CV) 개념을 활용하여 유체의 행동을 분석하는 것은 필수적입니다. 특히, 미소체적 내에서 압력을 계산하는 방법은 유체역학의 기초적이면서도 핵심적인 부분입니다. 여기서는 Control Volume으로 잡은 미소체적의 Side 부분에서 작용하는 압력 계산에 대해 설명하겠습니다.

Control Volume(CV)은 유체 흐름을 분석하기 위해 가상으로 설정하는 고정된 공간이나 체적을 말합니다. 이 공간을 통과하는 유체의 행동을 분석함으로써 유체의 속도, 압력 등 다양한 물리적 성질을 예측할 수 있습니다. 특히, 미소체적을 Control Volume으로 설정하여 유체의 미세한 변화를 관찰하는 것은 유체역학에서 흔히 사용되는 방법입니다.

미소체적 내 압력 계산의 이해

미소체적 내에서의 압력 계산을 이해하기 위해, 우선 유체의 흐름을 따라 작은 Control Volume을 설정합니다. 이 CV의 양 끝에서 작용하는 압력의 차이에 의한 힘은 AΔp입니다. 여기서 A는 면적이고, Δp는 압력의 변화량입니다. 이때 주목해야 할 부분은 흐름 방향에 따른 순압력을 구하는 과정입니다. Control Volume의 양끝에서 작용하는 압력 차이에 의해 발생하는 순압력 F_s,press는 다음과 같이 표현할 수 있습니다.

\[F_{s,press} = A\Delta p\]

이 공식에서 \Delta p는 압력의 변화량을 나타내고, 이 변화량에 의한 순압력은 -A\Delta p로 근사됩니다. 여기서 마이너스 부호는 압력이 감소하는 방향을 나타냅니다.

압력 계산에서의 면적 변화(dA)의 역할

질문에서 언급된 바와 같이, 1/2 * dp * dA라는 식이 이해가 되지 않는 부분에 대해 설명하겠습니다. 실제로 이 표현은 Control Volume 내에서 압력 변화를 나타내는 데 사용되는 근사 방법 중 하나입니다. 유체 흐름을 따라가며 압력이 변화함에 따라, 이 변화량을 면적 변화량 dA에 적용하여 압력 힘을 계산하는 것입니다. 이 과정에서, 압력 변화에 의한 면적 변화를 고려하여 미소체적 내에서의 순압력을 계산할 때 사용됩니다.

결론적으로, 1/2 * dp * dA라는 표현은 면적 변화에 따른 압력의 변화를 고려하는 근사 방법이며, 이를 통해 Control Volume 내에서의 압력 힘을 보다 정확하게 계산할 수 있습니다. 이러한 계산 방법은 유체역학에서 매우 중요한 개념 중 하나로, 유체의 흐름과 관련된 다양한 문제를 해결하는 데 기여합니다.

이미지를 통한 추가적인 이해를 위해, 여러분이 참고할 수 있는 이미지 링크를 첨부해드립니다.

유체역학의 세계는 매우 복잡하고 다양한 변수들이 상호작용합니다. 따라서, Control Volume을 이용한 미소체적 내 압력 계산 방법은 이러한 복잡한 현상을 이해하는 데 큰 도움을 줍니다. 질문에 대한 답변이 여러분의 궁금증을 해소하는 데 도움이 되었기를 바랍니다.

유니스터디 바로가기 : https://www.unistudy.co.kr/megauni.asp

학습Q&A 바로가기 : https://www.unistudy.co.kr/community/qna_list.asp