질문 요약
동역학 제대로 끝내기 3강에서 del(x(t))를 계산할 때, 미분 전에 대입하는 것과 미분 후에 대입하는 것의 차이는 무엇인가요?
답변 요약
오일러-라그랑주 방정식을 증명하는 과정에서 t1 또는 t2에 해당하는 변수 x가 상수이며, 이를 미분하면 0이 되는 이유는 해당하는 항이 사라지기 때문입니다. 식을 유도하면서 해당하는 항이 0이 되는 이유를 이해하시면 됩니다. [이미지](https://godjunpyo.com/wp-content/uploads/kboard_attached/8/202310/6525442356bba8498123.png)
Unsplash 추천 이미지 (키워드 : dynamics, calculation, differentiation before, substitution, differentiation afterward, difference, Euler-Lagrange equation, proof process, t1, t2, variable x, constant, differentiation, 0, reason, corresponding term, disappear, derivation, explanation, picture, link )
동역학 제대로 끝내기 3강에서의 del(x(t)) 계산 방법
안녕하세요, 동역학 제대로 끝내기 3강에서 del(T)를 유도하는 과정에 대해 궁금해하시는 분들을 위해 이 포스트를 작성하게 되었습니다.
먼저, 우리가 의문을 가지게 될 만한 부분을 살펴보겠습니다. 3강에서 del(T)를 유도하는 과정에서 del(x(t_1))와 del(x(t_2))를 계산할 때, x(t_1)와 x(t_2)가 상수인 것으로 봅니다. 그리고 상수를 미분하면 0이므로 del(x(t_1))=del(x(t_2))=0이라고 설명하였습니다.
그런데 여기서 의문이 생기는 부분은 적분 과정을 보면 del(x(t))를 먼저 구하고 t_1과 t_2를 구한 것으로 보이는데, del(x(t))에 t_1와 t_2를 대입하고 미분을 한다면 결과값은 0이 되겠지만, 미분을 먼저 하고 t_1과 t_2를 대입했을 때는 0이 아닐 수 있다는 것입니다.
예를 들어, y=x^2에서 2를 대입하고 미분하면 4를 미분하니 0이 되겠지만, 미분을 먼저하고 2를 대입하면 2*2=4가 됩니다. 이런 부분에서 어떤 부분이 문제인지를 알아보고자 합니다.
해결 방법
이 부분에 대한 해결 방법은 오일러-라그랑주 방정식을 증명하는 과정을 이해하는 것입니다. 이 과정에서 t1 또는 t2에 해당하는 변수 x가 상수이며, 이를 미분하면 0이 되는 이유는 해당하는 항이 사라지기 때문입니다.
즉, 식을 유도하면서 해당하는 항이 0이 되는 이유를 이해하시면 됩니다. 아래 그림을 참고하시면 이해에 도움이 될 것입니다.
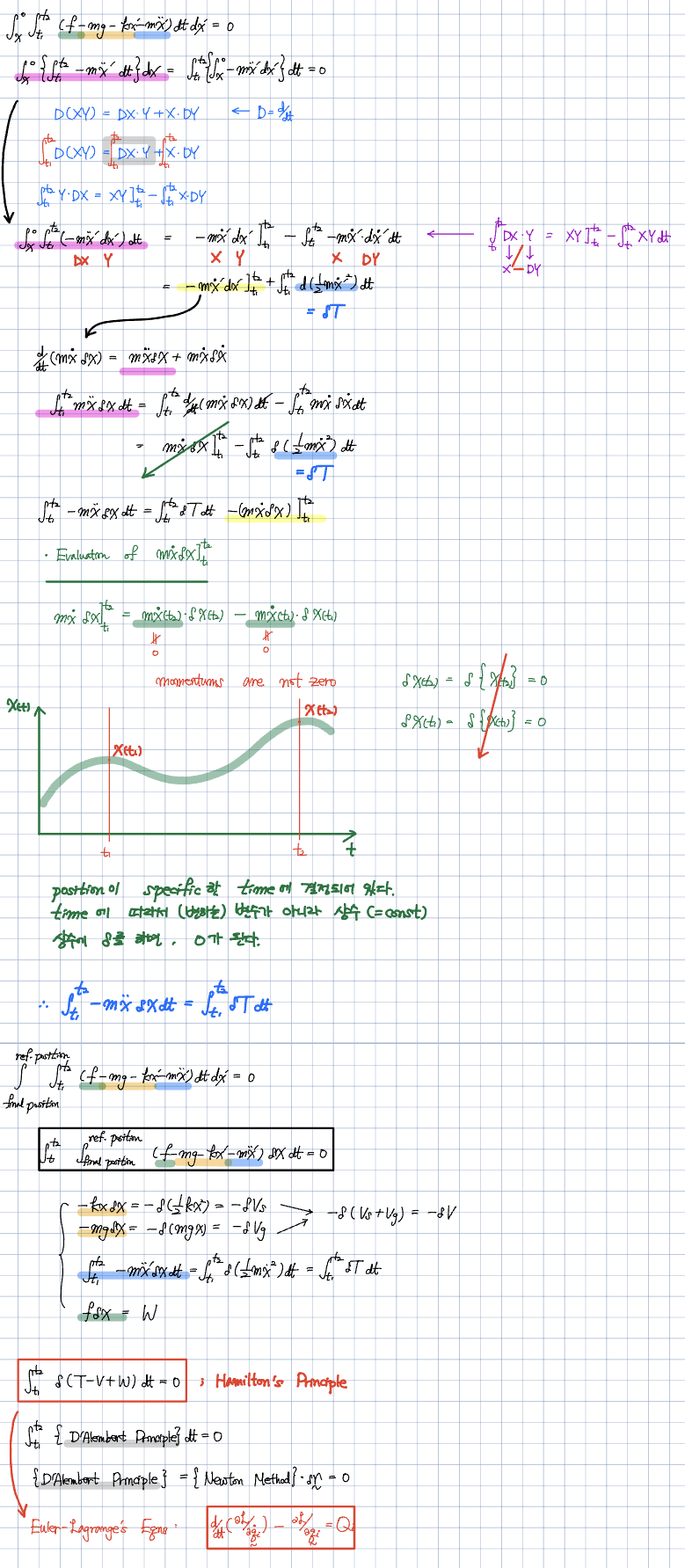
이렇게 오일러-라그랑주 방정식을 증명하는 과정을 이해하고 나면, 우리가 가진 의문에 대한 해결책을 얻을 수 있습니다. 미분을 먼저하고 t1과 t2를 대입했을 때와, 미분을 한 후에 t1과 t2를 대입했을 때의 차이는 이러한 원리에 근거한 것이므로 이를 이해하면 더 이상 혼동을 겪지 않게 될 것입니다.
이 설명이 동역학 제대로 끝내기 강의를 듣고 계시는 분들에게 도움이 되었길 바랍니다. 감사합니다.
유니스터디 바로가기 : https://www.unistudy.co.kr/megauni.asp
학습Q&A 바로가기 : https://www.unistudy.co.kr/community/qna_list.asp







0 댓글